Hoek-Brown Modell (HB)
Das Hoek-Brown Modell ist das am häufigsten verwendete Versagenskriterium zur Beschreibung des nichtlinearen Verhaltens von Gesteinsmassen. Ähnlich wie das Mohr-Coulomb Modell wird das Hoek-Brown Modell in Form von drei Versagensfunktionen mit der Projektion in den deviatorischen Raum in Form eines unregelmäßigen Sechsecks formuliert. Im Gegensatz zum Mohr-Coulomb Modell wird die Projektion der Fließfläche fHB in den Meridianraum durch eine nichtlineare Funktion beschrieben. Es ist offensichtlich, dass, ähnlich dem Mohr-Coulomb Modell, das Hoek-Brown Versagenskriterium eine Funktion des mittleren effektiven Stress σmeff und des Lode-Winkels θ ist.
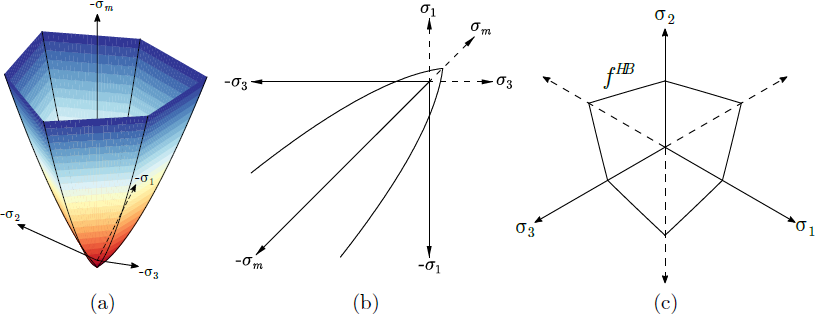a) Fließfläche im Hauptspannungsraum, b) Projektion in den Raum der maximalen und minimalen Hauptspannungen und c) Projektion in den deviatorischen Raum
Das Hoek-Brown Modell ist rein empirisch und seine Formulierungen basieren auf dem Geological Strength Index GSI (der Wert von of GSI =100 entspricht einem intakten Gestein und sinkt mit der Verschlechterung der Gesteinsqualität auf null). Der Störfaktor D (er berücksichtigt frühere unterirdische Aktivitäten, einschließlich Bergbau und Ausgrabung) ist ebenfalls ein Bestandteil des Modells. Der Wert von D=0 entspricht einem intakten Gestein, und der maximale Grad der Beschädigung wird durch den Wert D=1)dargestellt. Die uniaxiale Druckfestigkeit eines intakten Gesteins ist durch σci und den Parameter mi. gegeben. Diese beiden Parameter werden aus dem Triaxialtest bestimmt. Der physikalisch akzeptable maximale Wert der festgelegten Zugfestigkeit 
wird durch:
wobei der Parameter s und die reduzierte Hoek-Brown-Konstante mb in Bezug auf die Parameter GSI und D wie folgt ausgedrückt werden:
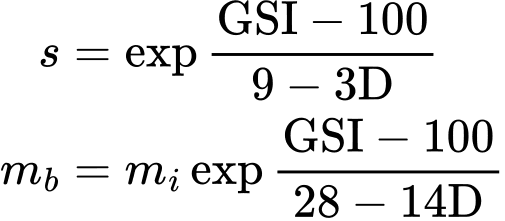
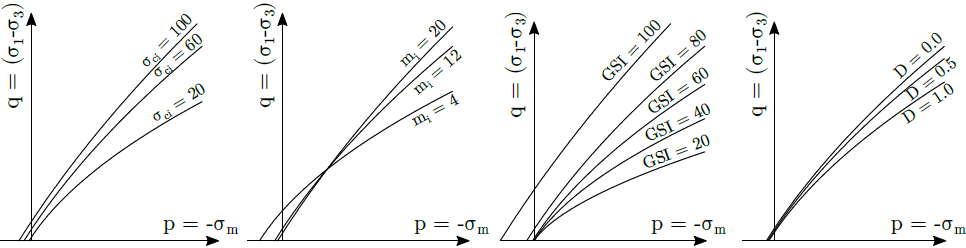
Die Auswirkung der einzelnen Parameter auf die Projektion der Fließfläche in den Meridianraum wird in der folgenden Abbildung veranschaulicht.
Das Hoek-Brown Modell erfordert die Einführung des Elastizitätsmoduls des Gesteinsmasses Erm, das den Schadenstatus der Gesteinsmasse berücksichtigt. Es kann beispielsweise mit Hilfe der Modellparameter GSI, D und σci bestimmt werden [2].
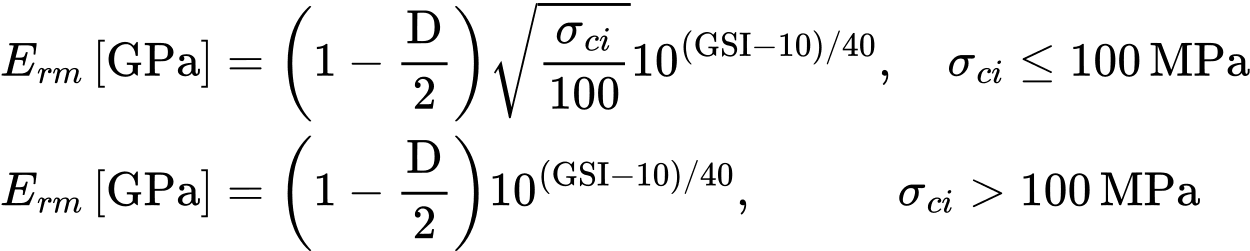
Weitere Optionen sind in [3] verfügbar. Der Modellparameter a ,der die Potenzbeziehung in der Definition der Fließfläche anpasst, kann ebenfalls unter Verwendung des Geological Strength Index GSI wie folgt bestimmt werden:
Die Modellparameter werden in der folgenden Tabelle dargestellt:
Symbol | Einheiten | Beschreibung | |
| [MPa] | Elastizitätsmodul des Gesteinsmasses | |
| [-] | Poisson-Verhältnis | |
| [MPa] | Druckfestigkeit im einachsigen Kompressionsversuch | |
| [-] | Hoek-Brown-Konstante | |
GSI | [-] | Geological strength index | |
D | [-] | Störfaktor | |
| [°] | Dilatanzwinkel (der anfängliche Wert | |
| [kN/m3] | Schüttgewicht | |
| [-] | Reduzierte Hoek-Brown-Konstante (spezifiziert oder berechnet aus GSI, D, | |
| [-] | Materialkonstanten (spezifiziert oder berechnet aus z GSI, D) | |
| [kPa] | Maximal zulässige Zugfestigkeit, | |
TsRF | [-] | Zugfestigkeitsreduktionsfaktor (0,1), falls spezifiziert dann | |
| [kPa] | Begrenzungswert des eingeschlossenen Drucks zur Modellierung der Dilatanz | |
| [1/K] | Wärmeausdehnungskoeffizient (wenn Temperatureffekte berücksichtigt werden) |
wird spezifiziert, siehe Abbildung)
)
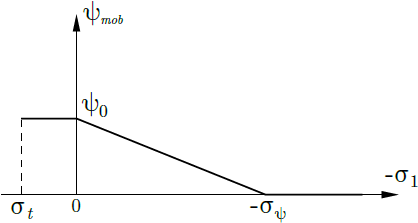
Die Fließregel ist ähnlich wie bei den Drucker-Prager- und Mohr-Coulomb-Modellen, allgemein nicht assoziiert. Daher ermöglicht sie die Modellierung der Dilatanz (Entwicklung positiver volumetrischer plastischer Dehnungen) durch die Einführung des Dilatanzwinkels ψ. Der Dilatanzwinkel ist jedoch nicht unbedingt konstant, sondern kann sich entwickeln, wie in der folgenden Abbildung dargestellt.
Die Implementierung des Hoek-Brown-Modells führt automatisch den Wert der maximalen Zugfestigkeit 
ein. Dieser Wert kann entweder angegeben oder anhand des Zugfestigkeitsreduktionsfaktors TsRF berechnet werden (siehe die Tabelle der Modellparameter). Die Begrenzung der Zugfestigkeit wird, ähnlich wie beim Mohr-Coulomb-Modell, durch die Rankin-Fließfläche gesteuert.
Sowohl die Standard-Stabilitätsanalyse als auch die Stabilitätsanalyse innerhalb einer gegebenen Bauphase können durchgeführt werden.Jedoch, im Gegensatz zum Mohr-Coulomb-Modell, führt das Hoek-Brown-Modell den Parameter η ein, um die einachsige Druckfestigkeit σci zu reduzieren. Dieser Parameter wird in Bezug auf den Reduktionsparameter ζ ausgedrückt, was in der Mohr-Coulomb-Modell die Scherfestigkeitsparameter φ, c reduziert. Der Sicherheitsfaktor FS wird daher gleich ζ gesetzt. Weitere Details finden Sie im theoretischen Handbuch.
Häufig gestellte Vergleiche mit dem Mohr-Coulomb-Modell werden im Detail hier beschrieben.Die Antwort des Hoek-Brown-Modells im Vergleich zum Mohr-Coulomb-Modell wird im theoretischen Handbuch durch einfache Laborversuche veranschaulicht.
Implementierung des Hoek-Brown-Modells in das GEO5 FEM-Programm wird im theoretischen Handbuch detailliert beschrieben. Weitere Informationen sind in der folgenden Literatur verfügbar:
Literatur :
[1] E. Hoek and E.T. Brown, Practical estimates of rock mass strength, International Journal of Rock Mechanics and Mining Sciences, 34.8 (1997), 1165-1186
[2] E. Hoek, C. Carranza-Torres and B. Corkum, Hoek-Brown failure criterion - 2002 edition, Proceedings of the 5th North American symposium - NARMS-TAC (2002)
[3] E. Hoek, M.S Diederichs, Empirical estimation of rock mass modulus, International Journal of Rock Mechanics \& Mining Sciences, 43 (2006), 203-215