Nachweis nach AISC 360-22 (LRFD, ASD)
Nachweis der Querkraft
Der Schubwiderstand für einen Verbundquerschnitt mit einer ausbetonierten Stahlquerschnitt wird konservativ als Schubtragfähigkeit des Stahlprofils bestimmt.
Die Bemessungs-Querkraft für einen ausbetonierten Rundquerschnitt ergibt sich zu:
![]()
wo: | Av | - | Schubfläche des Stahlprofils (bei einem Rundquerschnitt entspricht dies 2As / π |
Fy | - | charakteristische Mindeststreckgrenze | |
Kc | - | konservativ mit 1.0 angesetzt | |
Ac | - | Betonquerschnittsfläche | |
fc' | - | charakteristische Betonfestigkeit (Druckfestigkeit) |
Der Nachweis der Querkraft erfolgt durch:
- for LRFD: Q / (Vn ϕv ) ≤ 1.0
- for ASD: Q / (Vn / Ωv ) ≤ 1.0
Nachweis der Druckkraft
Die Bemessungs-Druckkraft für einen ausbetonierten Stahlquerschnitt ergibt sich zu:
![]()
Die Bemessungs-Druckkraft eines „nicht-kompakten“ ausbetonierten Rundprofils ergibt sich zu:
wo: | As | - | Querschnittsfläche des Stahlprofils |
Ac | - | Querschnittsfläche des Betons |
Nenn-Drucktragfähigkeit eines „kompakten“ ausbetonierten runden HSS-Profils ergibt sich zu:
![]()
![]()
![]()
wo: | λp, λr | - | Verhältnis Breite zu Dicke gemäß AISC 360 und Tabelle I1.1a |
λ | - | Verhältnis Breite zu Dicke = D / t | |
D | - | Außendurchmesser eines runden HSS-Profils | |
t | - | Wanddicke eines runden HSS-Profils |
Die Bemessungs-Druckkraft eines „schlanken“ ausbetonierten Rundprofils ergibt sich zu:
![]()
wo: | Fn | - | kritische Knickspannung |
![]()
wo: | Es | - | Elastizitätsmodul des Stahls |
Die verfügbare Drucktragfähigkeit wird wie folgt ermittelt:
- für LRFD: Pc = Pn ϕc
- für ASD: Pc = Pn / Ωc
Nachweis der Biegung
Die Bemessungs-Biegemomententragfähigkeit wird aus dem Interaktionsdiagramm für die entsprechende Normalspannungsverteilung unter Berücksichtigung des Biegemoments bestimmt.
Für Verbundquerschnitte mit ausbetonierten Stahlprofilen wird folgende Normalspannungsverteilung angenommen:
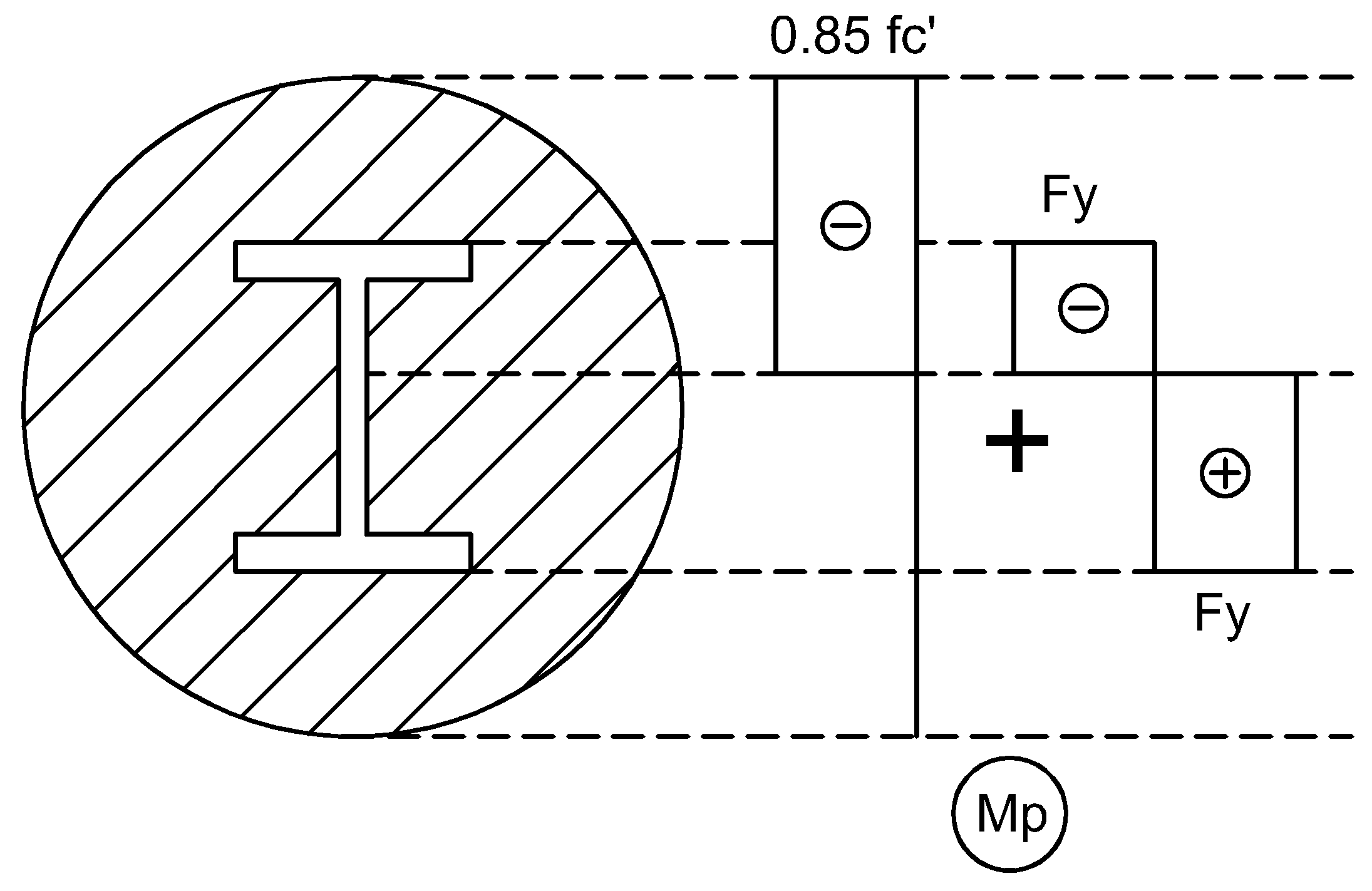
Die Bemessungs-Biegemomententragfähigkeit ergibt sich zu:
![]()
wo: | Mp | - | Moment entsprechend der plastischen Spannungsverteilung über den Verbundquerschnitt |
Für ausbetonierte runde HSS-Querschnitte wird je nach Verhältnis D/t die folgende Normalspannungsverteilung angenommen:
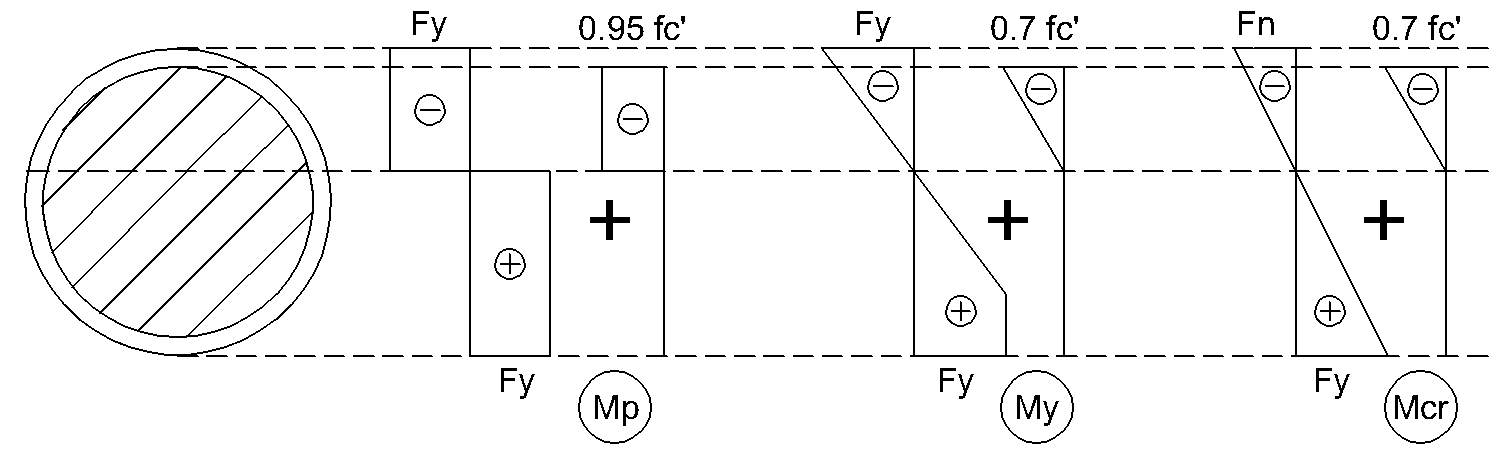
Die Bemessungs-Biegemomententragfähigkeit eines „kompakten“ ausbetonierten runden HSS-Profils ergibt sich zu:
![]()
Die Bemessungs-Biegemomententragfähigkeit eines „nicht-kompakten“ ausbetonierten runden HSS-Profils ergibt sich zu:
![]()
wo: | My | - | Fließmoment entsprechend der elastisch-plastischen Spannungsverteilung über den Querschnitt |
λp, λr | - | Breite-zu-Dicke-Verhältnisse gemäß Tabelle I1.1b |
Die Bemessungs-Biegemomententragfähigkeit eines „schlanken“ ausbetonierten runden HSS-Profils ergibt sich zu:
![]()
wo: | Mcr | - | erstes Fließmoment entsprechend der elastischen Spannungsverteilung über den Querschnitt |
Die verfügbare Biegemomententragfähigkeit wird wie folgt ermittelt:
- für LRFD: Mcx = Mn ϕb
- für ASD: Mcx = Mn / Ωb
Nachweis der Normalkraft und Biegung
Der Nachweis der Normalkraft und Biegung erfolgt mit folgenden Gleichungen:
- Falls : N / Pc ≥ 0.2
![]()
- Falls : N / Pc < 0.2
![]()